OCTAVO AÑO, "MATEMÁTICAS
Suma de números enteros positivos
Sumar números positivos no tiene mayor complicación. Tan sólo tienes que realizar la suma, igual que en el caso de sumar números naturales. Por ejemplo:
 Realmente lo que estás haciendo es sumar los valores absolutos de los números y después añadirle el signo más al resultado, o mejor dicho, dejarlo igual porque el signo más no se escribe.
Quédate con este concepto porque es clave para entender el siguiente apartado.
Realmente lo que estás haciendo es sumar los valores absolutos de los números y después añadirle el signo más al resultado, o mejor dicho, dejarlo igual porque el signo más no se escribe.
Quédate con este concepto porque es clave para entender el siguiente apartado.
Resta de números enteros negativos
Restar números negativos es un concepto que confunde mucho, porque nos cuesta mucho entender que el resultado sea más grande en valor absoluto que los números que estamos restando.
Para entenderlo mejor, vamos a realizar esta resta de números negativos:
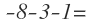 Para restar números negativos, tenemos que seguir el mismo procedimiento que para sumar números positivos: debemos sumar sus valores absolutos y después añadir el signo menos al resultado. Es decir, realizamos 8+3+1=12 y le añadimos el signo menos:
Para restar números negativos, tenemos que seguir el mismo procedimiento que para sumar números positivos: debemos sumar sus valores absolutos y después añadir el signo menos al resultado. Es decir, realizamos 8+3+1=12 y le añadimos el signo menos:

Paréntesis en los números enteros
En general, los números negativos se representan con el signo menos delante:
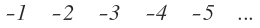
Como ya tienen un signo, cuando realizamos operaciones con ellos, si los escribiéramos así, tal cual, sin añadirles nada más, crearía confusión al tener dos signos seguidos, como por ejemplo en esta suma:
 Por eso, es necesario encerrarlos entre paréntesis, para distinguir entre el signo de la operación y el signo del número negativo:
Por eso, es necesario encerrarlos entre paréntesis, para distinguir entre el signo de la operación y el signo del número negativo:
 Por otro lado, también podríamos encerrar entre paréntesis los números positivos:
Por otro lado, también podríamos encerrar entre paréntesis los números positivos:
Por otro lado, también podríamos encerrar entre paréntesis los números positivos:
Por otro lado, también podríamos encerrar entre paréntesis los números positivos:
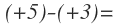 Pero como normalmente el signo positivo no se escribe, no es necesario encerrarlos entre paréntesis, ya que no tendríamos el problema de tener dos signos seguidos:
Pero como normalmente el signo positivo no se escribe, no es necesario encerrarlos entre paréntesis, ya que no tendríamos el problema de tener dos signos seguidos:

Como ya tienen un signo, cuando realizamos operaciones con ellos, si los escribiéramos así, tal cual, sin añadirles nada más, crearía confusión al tener dos signos seguidos, como por ejemplo en esta suma:
Multiplicación de números enteros
Para multiplicar números enteros se siguen los siguientes pasos:
- Se multiplica el signo, siguiendo la regla de los signos
- Se multiplican los números
Veamos un ejemplo: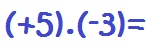 1. Multiplicamos los signos: Más por menos es menos:
1. Multiplicamos los signos: Más por menos es menos:
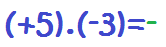 2. Multiplicamos los números: 5.3 = 15:
2. Multiplicamos los números: 5.3 = 15:
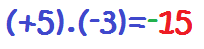 Y ya estarían multiplicados los números enteros. De la misma forma, multiplicaríamos estas otras multiplicaciones:
Y ya estarían multiplicados los números enteros. De la misma forma, multiplicaríamos estas otras multiplicaciones:
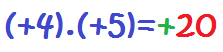
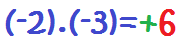
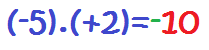
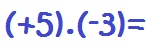
Y ya estarían multiplicados los números enteros. De la misma forma, multiplicaríamos estas otras multiplicaciones:
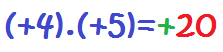
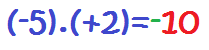
División de números enteros
Para dividir números enteros seguiremos los siguientes pasos:
- Se divide el signo, teniendo en cuenta la regla de los signos
- Se dividen los números
Veamos otro ejemplo de cómo dividir números enteros:

Dividimos los signos: Más entre menos es menos:
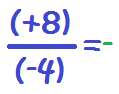
2. Dividimos los números: 8/4=2:
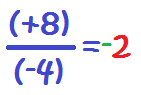
Y ya tenemos nuestra división de números enteros.
Aquí tienes otros ejemplos, con los otras combinaciones de signos que puedes encontrarte:
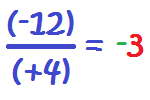
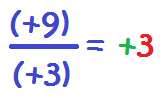
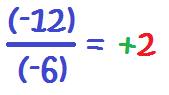
Puedes encontrarte con que el signo menos está delante de la fracción. En ese caso, el signo menos puede estar en el numerador o en el denominador indistintamente, ya que no varía el resultado:
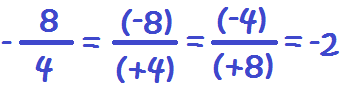
Suma y resta de números racionales
Con el mismo denominador
Se suman o se restan los numeradores y se mantiene el denominador.




Se suman o se restan los numeradores y se mantiene el denominador.




Con distinto denominador
En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.




En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.




Multiplicación de números racionales


División de números racionales


Ejercicios
DÉCIMO AÑO, MATEMÁTICAS
¿QUÉ SON LAS POTENCIAS?

Las potencias son una forma de abreviar una sucesión de multiplicaciones de un mismo número por sí mismo que se representa como xy, por ejemplo:
2 · 2 · 2 · 2 = 24 = 16
Se denomina:
- base. Al número que se multiplica (x) un determinado número de veces. En el ejemplo anterior la base sería el 2.
- exponente. Al número de veces (y) que se multiplica la base. En nuestro caso sería el 4.
Así, podemos sustituir 2 · 2 · 2· 2 por 24 y se leería 2 elevado a 4.
Propiedades de las Potencias de Exponente Entero
A continuación mostramos algunas de las operaciones básicas que se pueden realizar con las potencias.
Potencia con exponente 0
Cualquier número elevado a 0 da es igual a 1 (la unidad)
Ejemplo.
Cualquier número elevado a la unidad (1) da como resultado ese mismo número
Ejemplo.
Una potencia elevada a otra potencia es igual a otra potencia que:
- tiene la misma base
- el exponente es el producto de los 2 exponentes.(
Ejemplo.
Producto de Potencias con la misma base
El producto de dos potencias que tienen la misma base da como resultado otra potencia que:
- tiene la misma base
- y su exponente es la suma de los exponentes de ambas potencias
Ejemplo.
Producto de Potencias con distinta base y el mismo exponente
El producto de dos potencias que no tienen la misma base aunque si el mismo exponente de como resultado otra potencia cuya:
- base es el producto de las bases de ambas potencias.
- el exponente es el mismo que el de ambas potencias.
Ejemplo.
División de Potencias con la misma base
La división de dos potencias con la misma base da como resultado otra potencia que:
- tiene la misma base que las dos anteriores
- y su exponente es la resta de los exponentes de ambas potencias.
Ejemplo.
División de Potencias con distinta base y el mismo exponente
La división entre dos potencias que no poseen la misma base y sus exponente son iguales, da como resultado otra potencia cuya:
- base es la división de las bases de ambas potencias
- el exponente es el mismo que el de ambas potencias
Ejemplo.

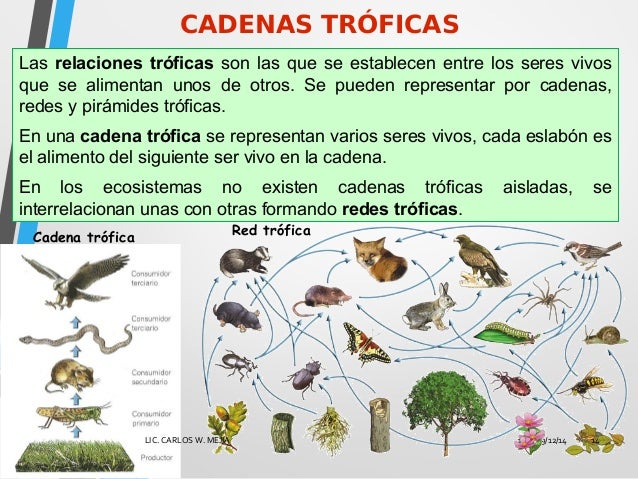
NOVENO AÑO, CIENCIAS NATURALES
DÉCIMO AÑO, EDUCACIÓN FÍSICA

DÉCIMO AÑO, CULTURA FÍSICA
ACTIVIDAD FÍSICA
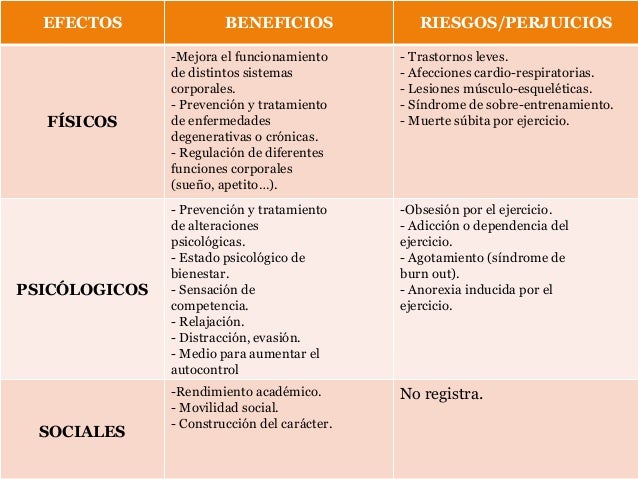

DÉCIMO AÑO, CULTURA FÍSICA
ACTIVIDAD FÍSICA









No hay comentarios:
Publicar un comentario